Software¶
Most of the software that I have written can be found on Github. Here is some additional information about some of my larger projects.
Twister¶
Twister is a program by myself, Tracy Hall and Saul Schleimer for constructing triangulations of surface bundles and Heegaard splittings from a description of a mapping class of a surface. These mapping classes are given as a composition of Dehn twists on annuli and half twists on pairs of pants. Twister is included in SnapPy 1.3.10+ and this is how we recommend you use it. Alternatively, you can download Twister’s source code, which you can compile as a Python 2 module, Python 3 module or standalone program and whose documentation now includes a users guide. Twister is freely available under the GNU general public license.
Flipper¶
Flipper is a program for computing the action of mapping classes on laminations on punctured surfaces using ideal triangulation coordinates. It can decide the Nielsen–Thurston type of a given mapping class and, for pseudo-Anosov mapping classes, construct a layered, veering triangulation of their mapping torus, as described by Agol. It can now also determine the conjugacy class of pseudo-Anosov mapping classes.
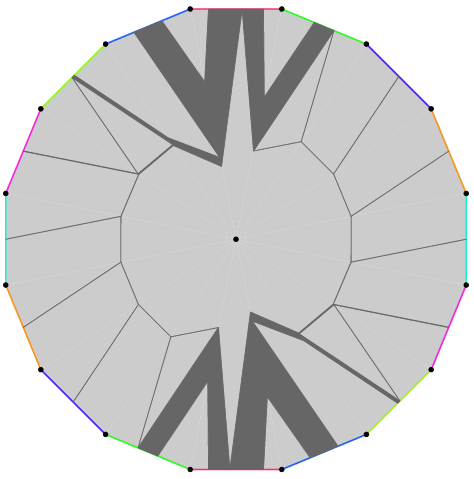
The stable lamination of a Penner like pseudo-Anosov.¶
Flipper is currently under development but you can install flipper from PyPI or from flippers source code.
Curver¶
Curver is a program for performing calculations in the curve complex. It implements the Bell–Webb algorithm to determine the Nielsen–Thurston type of a mapping class. This algorithm runs in polynomial time but the constants involved currently make this implementation impractical. It can now also determine the conjugacy class of periodic mapping classes.
Curver is currently under development but can you can install curver from PyPI or from curvers source code.
Bundler¶
One use for these pieces of software is to build censuses of surface bundles, for example knot complements. Software for generating such censuses can be found here. I am happy to discuss generating new censuses that people are interested in.
This works by first using Curver to efficiently enumerate the conjugacy classes of mapping classes for a given surface. Twister is then used to build a triangulation of the mapping torus of each mapping class and the manifold identified using SnapPy. Finally, for the bundles which SnapPy failed to find a hyperbolic structure, Flipper can verify that these examples are not pseudo-Anosov.
One use for these censuses was to search for fibred knot complement monodromies. The mapping class group of surfaces S_{g,1} with \(1 \leq g \leq 5\) were searched to depths shown in the table below. Knot complements were then identified and compared to each of the fibred knot complement listed on knotinfo.
Genus
1
2
3
4
5
Depth
2
10
14
14
14
As of March 2013, monodromies were found for approximately 63% of the knots listed and as shown in this summary. This monodromy data is now also part of knotinfo. Note that, the list of fibred knot complements built was a complete census. Therefore if a monodromy was not found for a particular knot then it cannot have a monodromy consisting of 2 / 10 / 14 / 14 /14 or fewer characters (depending on its three genus).
Bigger¶
Bigger is a program for creating and manipulating big mapping classes. It can create mapping classes on infinite-type surfaces and apply these to laminations with infinite support through lazy evaluation.
Bigger is currently under development but can you can install bigger from PyPI or from biggers source code.